具体例で学ぶ数学 > 計算 > ルート(平方根)の意味と計算ツール 最終更新日 ある数 × ある数 = 別の数 が成り立つとき、 ある数 を 別の数 の平方根と言います。 例えば、 3 は 9 の平方根です。 目次 平方根(ルート)を計算するツール 正の在數學中,一個數 的平方根 指的是滿足 = 的數,即平方結果等於 的數。 例如,4和4都是16的平方根,因为 = = 。 任意非負實數 都有唯一的非負平方根,称为算术平方根或主平方根(英語: principal square root ),記為 ,其中的符号√称作根号。 例如,9的算术平方根为3,记作 = ,因为 = = 并且3非34 非循環小数にはのようなものもあるが、代表的なものは2の平方根であるや円周率がある。 循環小数の書き方は

数の分類 Inertia
負の数の平方根 分数
負の数の平方根 分数-例えば、9の平方根って何だろう。 9の「2乗する前の数」、言い換えると、 「2乗すると9になる数」 。 これは3だよね。 でも、それだけじゃないよ。(-3) 2 =9 だから、 -3も9の平方根 だ。平方根は負の実軸に沿った分枝切断線で不連続となる: Sqrt x ^2 を自動的に x に簡約することはできない: x が正であると仮定すると,簡約することができる:



1
負の数の平方根は(実数の範囲には)ない。 2 つ目の項目について、2 乗して 0 になる数は 0 だけなので、0 の平方根は 0 の 1 つだけとなります。1「根号を使わずに表す」問題の解き方について解説します。「ルートとは? ?」でも述べましたが, は「2乗して3になる数」,という意味合いでした。 aを正の数として, という式が成り立ちます。これを応用して (1) (2) (3) 2平方根についての正誤を問う問題は,入試にはほとんど出ません私たちの平方根 計算機は、これらの式と単純化手法を考慮して、任意の数または任意の分数の平方根を解きます。 分数の平方根: 分数のsqrtは、除算演算によって決定できます。次の例を見てください。 (a / b)^ 1/2 =√a/√b=√a/ b ここで、a / bは任意の
平方完成のやり方が分かればちょっとやりにくそうな平方完成をやっていってみましょう! まずは\(x^2\)の係数が負の数であるときの平方完成をしてみます。 例題をやってみましょう。 <例題> 平方完成しましょう。 \(x^24x5\) まずは\(x^2\)の係数を確認し平方根1_平方根を求める x 2 =A のとき xをAの 平方根 という。 正の数には平方根が2つ,0の平方根は0だけで,負の数には平方根はない, 解説動画 ≫ 次の数の平方根を求めよ。 25 1 4 6 ① 2乗して25になる数は 5と5なので 答 ±5 ② 2乗して 1 4 になるのは 1 2 と 1平方根にはマイナスの数もあるよ。 (1)の答え 分数の平行根もポイントは同じ。 ±√をつけよう。 ただし、√を外せるときには注意して! 分母の25と分子の4、はそれぞれ2乗のカタチにできるよね。 (2)の答え 12 2 =144だよ。 このほかに
平方根の掛算・割算 平方根を素因数分解で解する方法 平方根の足算・引算 # 同じ数の平方根の足算・引算は、まとめて計算できます。 有理化 # 分母に平方根が含まれる時、分母が整数となるように式を変形することを、『分母を有理化する』という順序数を用いて位置関係を表 すこと 11,12の数え方,よみ方 4 いくつといくつ 10までの数の構成(合成・分解) 1つの数をほかの数の和や差と してみること 9 10より大きいかず までの数の数え方, よみ 方,書き方 までの数の構成,大小,系列25の平方根は5と−5 の2つですが,そのうちの負の方を で表します. だから, です. 正の数 a に対して, a の平方根をまとめて で表し,プラス・マイナス・ルート a といいます. 例9 9の平方根は すなわち です. 例10 25の平方根は すなわち です.



Www Junten Ed Jp Contents Wp Content Uploads 13 04 8dc65ed5b5dbd2951eb8 Pdf




数と式 平方根について 日々是鍛錬 ひびこれたんれん
補足 平方根と立方根 平方根 多くの皆さんは平方根とかルート(根号) のことを知っていると思います そういう人はこの セクションを飛ばして下さい x2 = a を満たすx, 即ち2 乗(平方) してa になる数をa の平方根といいます 例4の平方根は2 と−2, 9 の平方根高校講座HOME >> ライブラリーTOP >> 数学Ⅱ 数学Ⅱ 出演者紹介 年度に放送した「NHK高校講座」の再放送です。 全科目・全回を各1回、年10分数(有理数)の指数が付いている式は累乗根で表される式と同じものです.多くの場合,分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります. 分数(有理数)の指数の定義 a>0 であって m, n が正の整数であるとき a mnn = n√



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




複雑なルートの分数の有理化のやり方と問題 理系ラボ
負の数の平方根 a > 0 a > 0 のとき、 √−a = √ai − a = a i とする。 また、 −a − a の平方根は、 ±√ai ± a i とかける。 つまり、 √−3 = √3i − 3 = 3 i であり、 −8 − 8 の平方根は ±√−8 = ±2√2i ± − 8 = ± 2 2 i となります。 目次 1 数学分数や小数の平方根(へいほうこん)って、どうやって求めるの? 平方根 中3 中学数学 11 分数の平方根を求める 12 整数の平方根を求めるとき、なぜ、素因数分解をするのか 13 小数の平方根を求める スポンサーリンク スポンサー平方根の大小 まとめ お疲れ様でした! 平方根の大小関係を比べるときには それぞれの数をルートの形に変形して 中身の大小を比較してやります。 入試では(10)(11)のような 範囲を与えられる問題が多いですが 考え方は非常にシンプルです。




中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく




2の平方根 Wikipedia
平方根の大小は?分数、負(マイナス)の数との関係 平方根の大小は「√の中の数」で判断できます。また「√が付いていない値」は、√の値に変換して大小を確認できます。 平方根とは?1分でわかる意味、ルート、求め方、覚え方、公式と問題 根号と虚数の平方根 正の数 の平方根,すなわち の解は 異なる つの実数,正と負 例 の平行根は 負の数 の平方根,すなわち の解は 異なる つの純虚数,互いに共役 100の平方根は10と-10です。 負の数も平方根になるので、忘れないでください。 わかりましたか? 理解できたかどうか、 例題で確認しましょう。 例題 平方根 次の数の平方根を答えてください。 (1)36 (2)049 (3)4/81 (4)0



Happylilac Net Pdf Jhs Math3 02 01ans Pdf




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月
数学ワークシート 平方根(2) 月 日 正方形の1辺の長さをx とすると ① ② ③ ④ ⑤ ⑥ 1 次の数の平方根をいいなさい。 (1) 25 (2)1 (3)81 (4)49 (5) 16 (6) (7)036 (8)009 9 4 1数の演算法則 平方根とルート 一次不定方程式 ガウス記号 n進法 数・式 en ja 平方根 実数 a に対し a = b 2 となる b を a の平方根 正の実数 a の平方根のうち正のものを a とする 負の実数の根の形に分解できる 連立方程式を立てて未知数を決定すればb1 = b3 = b5 = b6 = 0, b2 = 1, b4 = 1 を得る 実は, この被積分関数では変数tはt2 の形でしか現れないので, s = t2 と置いてから部分分数分解してもよい 部 分分数分解の一般論によれば, この場合は, s (1s)3



1



対称式 平方根通分ルートのある分数の通分の仕方を教えてください Yahoo 知恵袋
以下に平方根の定義をまとめる。 正しく理解できているか、もう一度確認してほしい。 2乗すると A になる数 を A の平方根といい、正のものと負のものの2個存在する。 これらのうち、 正の方を A 、 負の方を − A と表す。 また、 0 の平方根は 0 のみで50 2章 平方根 平方根の表し方を考えよう。 正の数a の平方根には,正の数と負の数の2つがある。 これらの平方根を,記号 を使って次のように表す。 正のほうを a,負のほうを- 0の平方根は0だから, 0=0である。 を使って平方根を表す16の平方根は± 16 =±4 2の平方根は± 2 15の平方根は± 15 xの平方根は± x 負の数には平方根が存在しないので 根号の中は必ず正の数 である。 上の例で言うとxは必ず正でなければならない。 a 2 の平方根 ( ) 2 = A のとき に入る数をAの平方根という
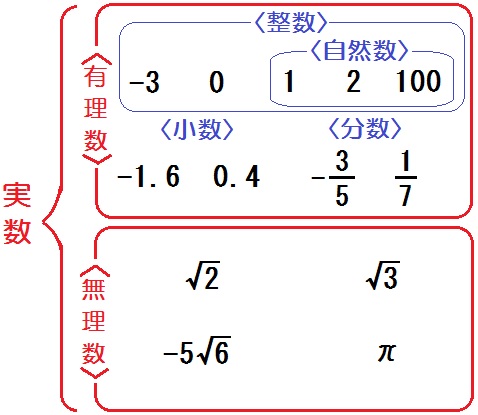



中学数学 平方根 のコツ 有理数と無理数 循環小数と分数




これで完璧 平方根の基礎 中3数学 中学生の勉強法
分数の平方根 次は分数の平方根について考えていきましょう。 \(\displaystyle \frac{9}{16}\)の平方根は? 分数だからといって、特別な考え方をするわけではありません。 分母と分子の数についてそれぞれ考えていけば良いだけです。 今回の場合2の平方根は、後述するように無理数である。2 の平方根は、人類の歴史において極めて初期の段階で発見されており、おそらく最初に知られた無理数であると考えられている。幾何学的には、1辺の長さが 1 の正方形の対角線の長さに相当する。数の範囲を,いままでみてきたような複素数にまで拡張すれば,負の数の平方根を求めることができる. 例として, − 3 の平方根を求めてみよう. つまり, − 3 の平方根は √3i と − √3i である. 一般には次のようにまとめられる.
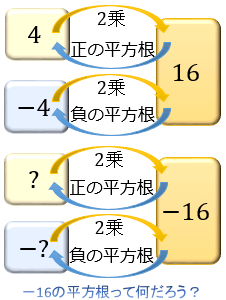



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




正の数や負の数の乗法や除法 割り算が出たら掛け算に戻す習慣を 中学や高校の数学の計算問題
記号 を「 根号 」といいます。 正の数も負の数も 2乗すれば正の数 になります。 2乗して負の数になる数はないので、 負の数の平方根はありません 。 (高校の数学では、負の数の平方根も扱います。 ) なので、 の平方根は です。 注意 の平方根は平方根を計算することは、x 2 =aとなるxの値を求めることになります。 また、中学校では a が0以上の数である場合のみを勉強します。 なぜなら、2乗して負の数になる数は存在しないからです。 ※ 高等学校では、2乗して負になる数も学習します(虚数)数Ⅱの負の平方根の説明動画です。次 8判別式 https//youtube/pWn0U0290VE前 6複素数 https//youtube/DrDx7QrnvjsTwitter https//twittercom




中1数学 正負の数 小数 分数の正負の数 たし算 Youtube
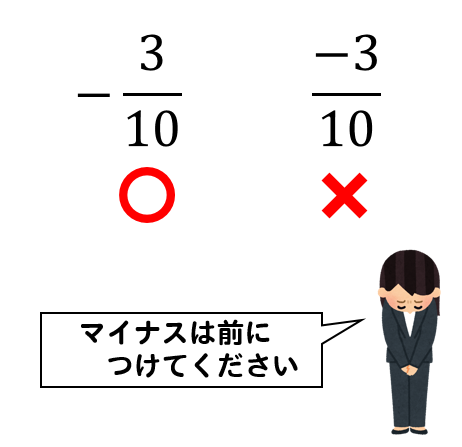



中1数学 正負の数 分数計算のやり方を問題解説 数スタ
「平方根」というのは2つあります。 たとえば、 ・9の平方根は? と聞かれた場合、 ・2乗すると9になる数は? という意味なので、 「+3と、-3」 の 2つの答えがあります。 (ここまではもう大丈夫ですね!) 同じことを根号(ルート)で表せば、したがって9の平方根=±3になります。 平方根はプラスとマイナスの2つがあるので注意。 2乗して0になるものは0だけなので、0の平方根は0だけ。 2乗してマイナスになるものはないので、負の数の平方根は存在しない。 中学数学の範囲では、0 以上の数にしか平方根が存在しないことに注意しましょう。 ※ 0 の平方根は 0 のみです。 ルートとは いよいよルートの登場です。 ある数 a (a > 0) の平方根のうち負でないものを と書き、「ルート a 」と読みます。




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




Apple Booksで小 中 高の計算がまるごとできるを読む
例題1:9の平方根を求めなさい まずは「二乗したら9になる数字」を考えましょう。 数には正の数と負の数しか無いので選択肢は3×3か (3)× (3)となります。 では、どちらの計算結果が9になるでしょうか。 どちらも答えは9です。 この様に負の数に平方1巻: 1章 正の数・負の数 小学校の計算 2巻: 2章 文字式 2巻: 2章 平方根 3巻: 3章 2次方程式 ② 分数にはすべて、分数囲み記号を用いた。 (4)電卓について




高校 数学 複素数7 負の数の平方根 13分 Youtube




2乗して10になる数 はどう求める じつは分数でも書けます 横山 明日希 ブルーバックス 講談社 1 3



Http Www Kochinet Ed Jp Asagaoka J tankyu 2sugaku Pdf




中学数学1年 代入と式の値 受験の月
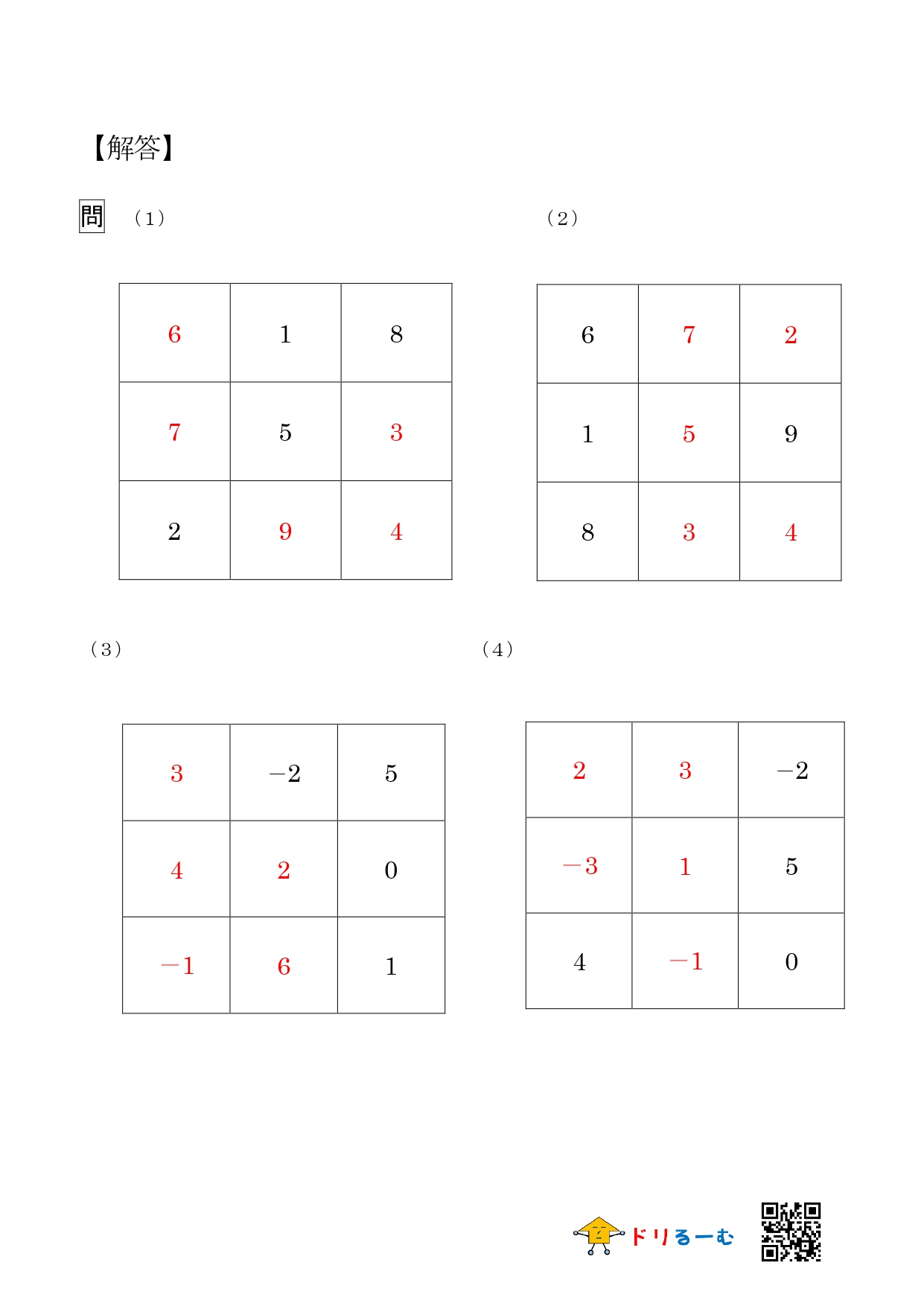



正の数 負の数 魔方陣 ドリるーむ




数学 時短演習cote




中学数学が秒でわかる 分数を数直線上に表す 図付き なぜか分かる はかせちゃんの怪しい研究室




2重根号の計算 数学 苦手解決q A 進研ゼミ高校講座




正負の数とは 数の表し方 反対の性質の表し方について解説 数スタ



Www Ariake Nct Ac Jp Wp3 Wp Content Uploads 04 9fc804d9fe761c4937b639d2aaa526 Pdf




絶対値とは 絶対値の計算問題 意味や性質 分数の絶対値の外し方について解説 ルート 遊ぶ数学




中1 P 26 正負の数の計算特訓 Youtube




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学




いまさらながら 懐かしの 帯分数 について考えた Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中学1年数学 正の数 負の数 分数の足し算 引き算の解き方 分数とは何か からはじめよう 数学の面白いこと 役に立つことをまとめたサイト




平方根とルートの違い ルート外しの注意点 趣味の大学数学



自然数とは 1分でわかる意味 整数との違い ルート マイナスの数 0との関係




ルートなんて意味不明 の意味や特徴を理解しよう 平方根がない数ってあるの さびねこ中学校




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学



2乗 平方根




数と式 平方根について 日々是鍛錬 ひびこれたんれん




平方根の求め方って 分数や小数の時はどうしたら良いの さびねこ中学校



1



平方根って何 なぜ必要 まぜこぜ情報局




負の無限大への極限対策 怜悧玲瓏 高校数学を天空から俯瞰する




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数と式 平方根について 日々是鍛錬 ひびこれたんれん
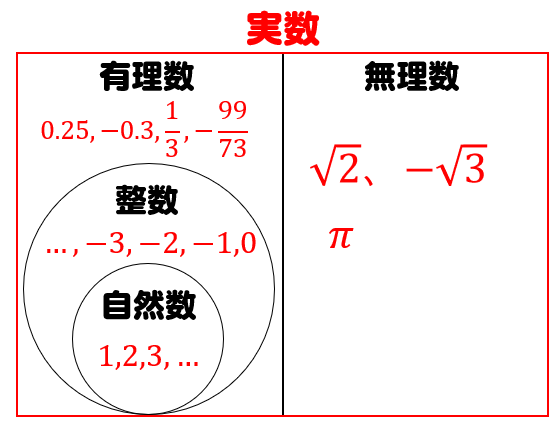



有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun




世界一わかりやすい数学問題集中1 1章 正の数 負の数




中学1年生 数学 正負の数 正の数 負の数 問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部



中学数学 平方根



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算




中学数学 問題 3 分数の計算 の入試過去問 厳選10問 基礎からのやり直し 苦手克服 復習ドリル 計算 問題集 行間 ぎょうのあいだ 先生




中学数学1年 正負の数の乗法と累乗の計算 受験の月




高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




正の数と負の数の加減乗除




数学 負の数の平方根の使い方とコツ 教科書より詳しい高校数学




平方根と指数 どこかの街の電気屋




平方根とは コトバンク




急ぎです 数 の複素数 負の数の平方根 3 2 3i 2i そ 数学 教えて Goo




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
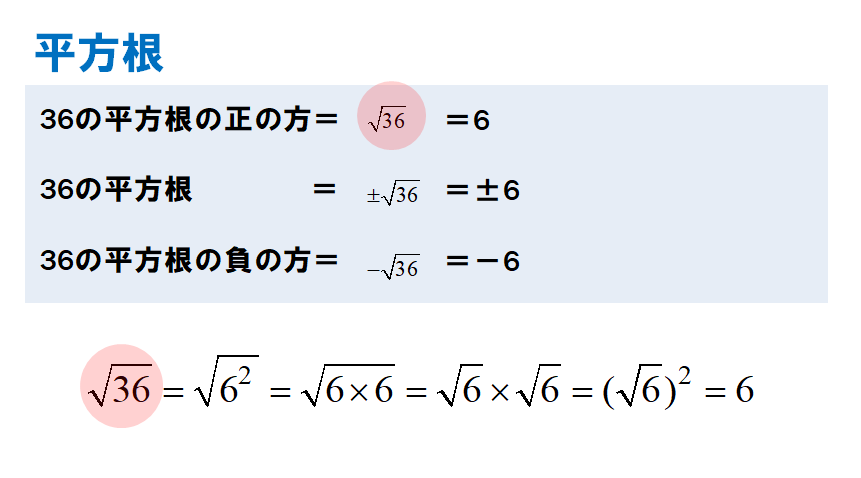



中3数学 平方根の性質の定期テスト対策問題 Examee




なんで分数が入ってくるのか分かりません Clear




Catatan Tentang テ対 数学 平方根 Junior High 数学 Clear




小 中 高の計算がまるごとできる 足し算 引き算から微分 積分までの通販 間地 秀三 紙の本 Honto本の通販ストア



Http Www Fdtext Com Dat Suub3 2kon 1kon Pdf




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



3




平方根 超簡単にわかる 有理数と無理数 苦手な数学を簡単に




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




正負の数から乗法公式まで一気に教える




中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会



数学 の複素数の負の数の平方根についてです なぜ Iぶ Yahoo 知恵袋




負の平方根 高校数学 Youtube




なぜ マイナスルート3は無理数なのですか 教えてください Clear




高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト



Q Tbn And9gcsrsyflswd5nekob2qdgwfj4wudlalz1 Ntjz0qpjnwmaqpfdla Usqp Cau




平方根とは さわやか さくらぐみ




中学校数学 3年生 数量 平方根 Wikibooks




これで完璧 平方根の基礎 中3数学 中学生の勉強法




平方根と指数 どこかの街の電気屋




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト



2




累乗 べき乗の計算機 指数が分数 小数 マイナスでもok やまでら くみこ のレシピ



平方根まとめ




数の分類 Inertia




平方根 ルート の値を求める計算機 分数もokな電卓サイト やまでら くみこ のレシピ
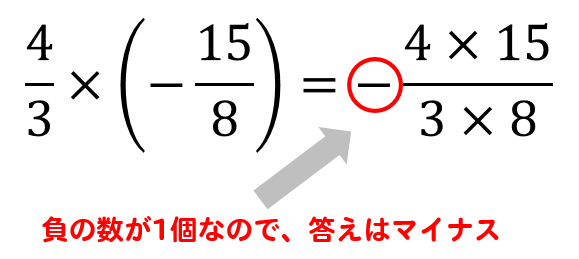



中1数学 正負の数 分数計算のやり方を問題解説 数スタ




โน ตของ 数学 ーーー 平方根 ーーー ช น Junior Clear




べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ



Www Kawai Juku Ac Jp Spring Pdf Text58 Pdf




中学数学 平方根 のコツ 平方根とは 平方根の大小



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
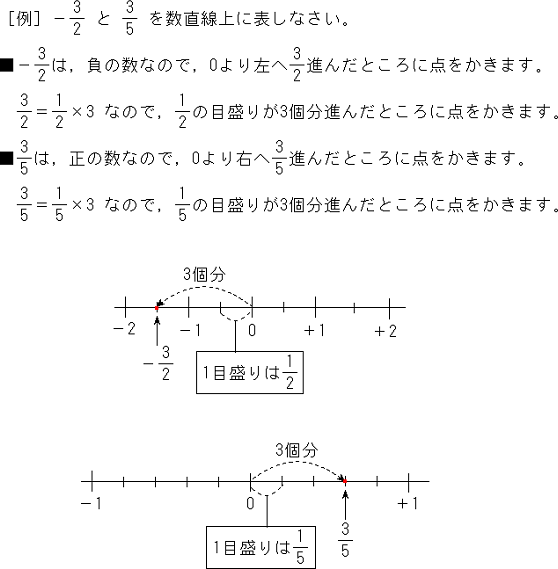



正負の数 分数の数直線上での表し方 中学数学 定期テスト対策サイト



マイナスのついた分数の累乗がわかりません 1 2 1 2 4 3 Yahoo 知恵袋




中1数学 正負の数 割り算 負の数で割る オンライン無料塾 ターンナップ Youtube




中学数学3年 平方根の計算 加法 減法 乗法 除法 と分母の有理化 受験の月




負の数の平方根 一夜漬け高校数学222 3の平方根は Youtube




正の数 負の数と四則演算 数学の要点まとめ 練習問題一覧




これで完璧 平方根の基礎 中3数学 中学生の勉強法
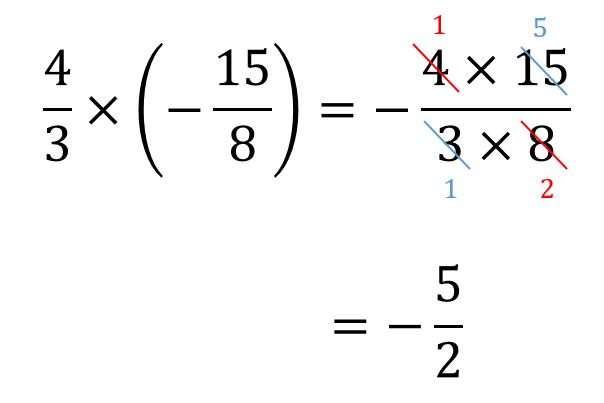



中1数学 正負の数 分数計算のやり方を問題解説 数スタ




数と式 平方根について 日々是鍛錬 ひびこれたんれん




世界一わかりやすい数学問題集中1 1章 正の数 負の数




中学数学 平方根 のコツ 有理数と無理数 循環小数と分数




中1数学 正負の数 分数計算のやり方を問題解説 数スタ



0 件のコメント:
コメントを投稿